微分方程式の解析解 in python

相平面ではベクトル場はこのように書ける

$$\begin{array}{r}\dot{x_1}=f_1(x_1,x_2)\\ \dot{x_2}=f_2(x_1,x_2)\end{array}$$

(x1, x2)は平面上の点を表し、ドットをつけるとその点における速度ベクトル 非線形系は解析的に解が得られない場合が多いので相図はかなり役にたつ

今回は課題に倣って

$$\begin{array}{r}\dot{R}=aR+bJ\\ \dot{J}=cR+dJ\end{array}$$

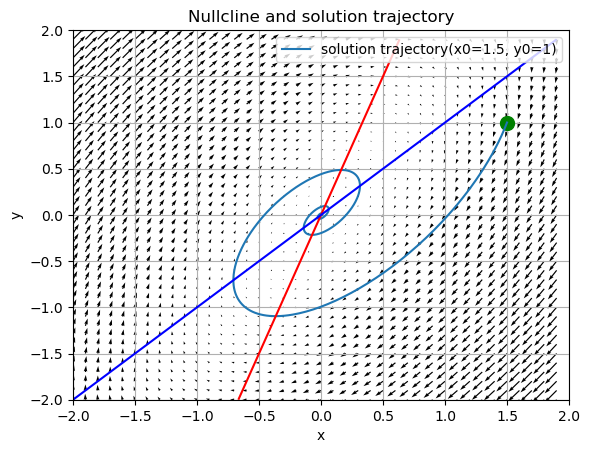
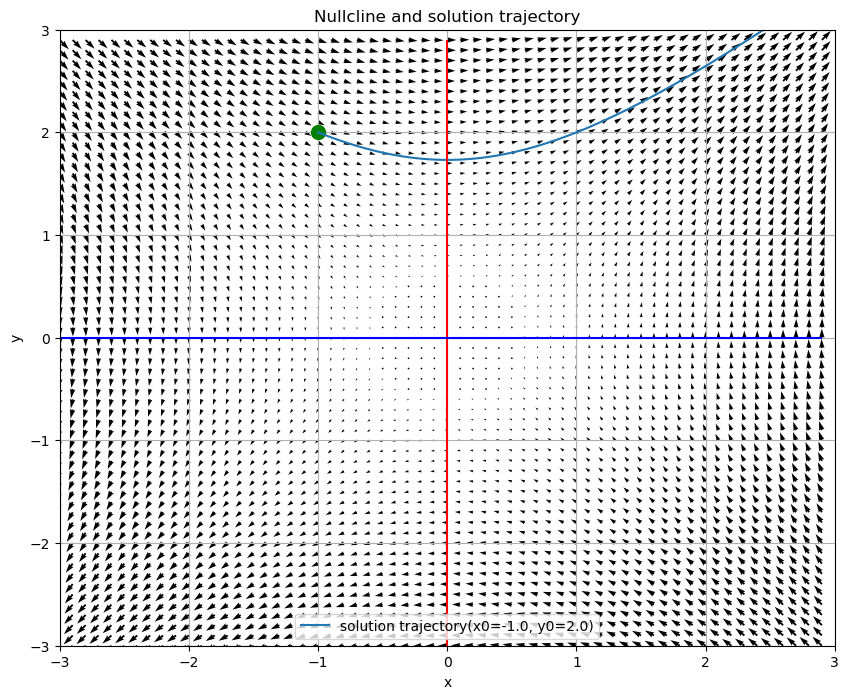
を扱ってみる この時の相図と、ベクトル場の様子は以下のようになる a=d=0, c, b = 1

上の図の濃い青、濃い赤で示したラインはヌルクラインといい $\dot{x}=0$または$\dot{y}=0$となる曲線である つまり微分値(速度)が0になる部分である

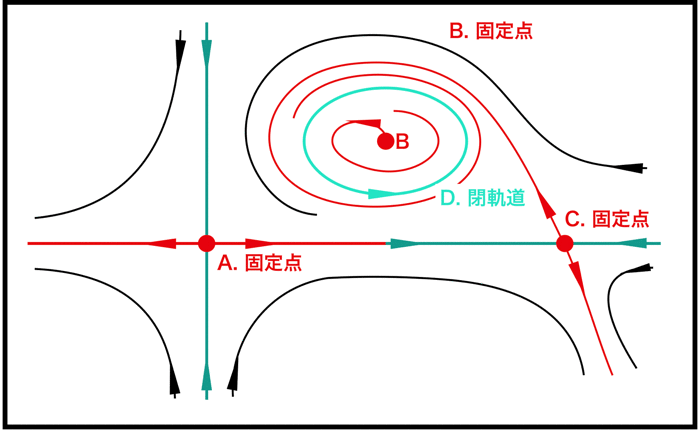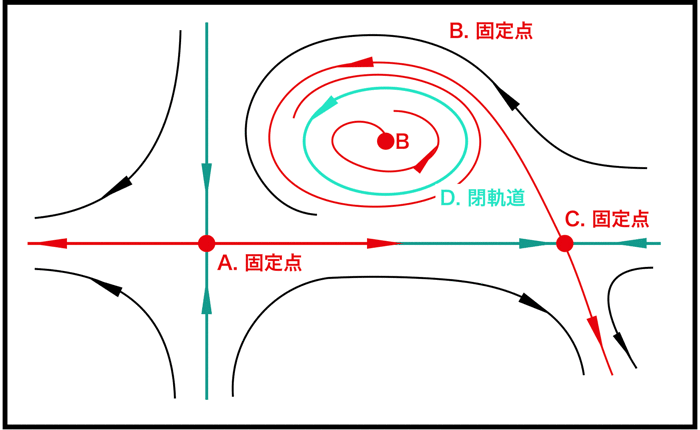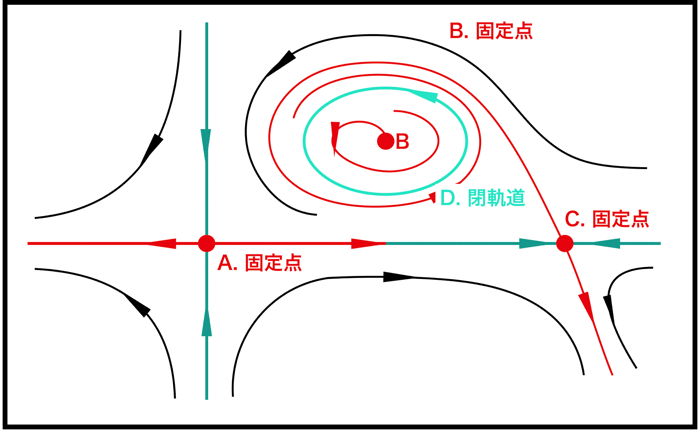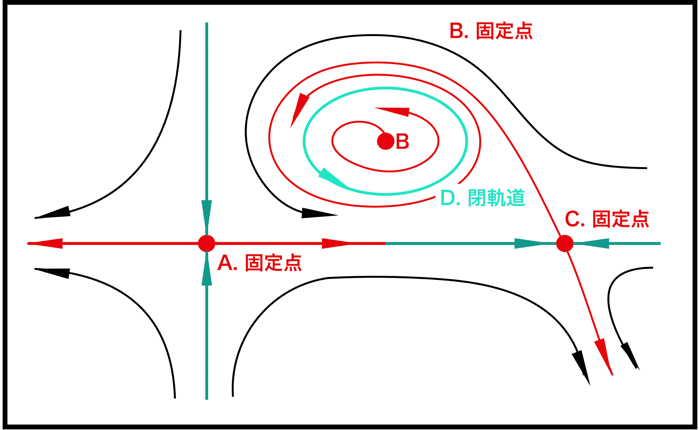
ここで図にあるような領域(または点)を初期値に与えて解軌道を描画してみる

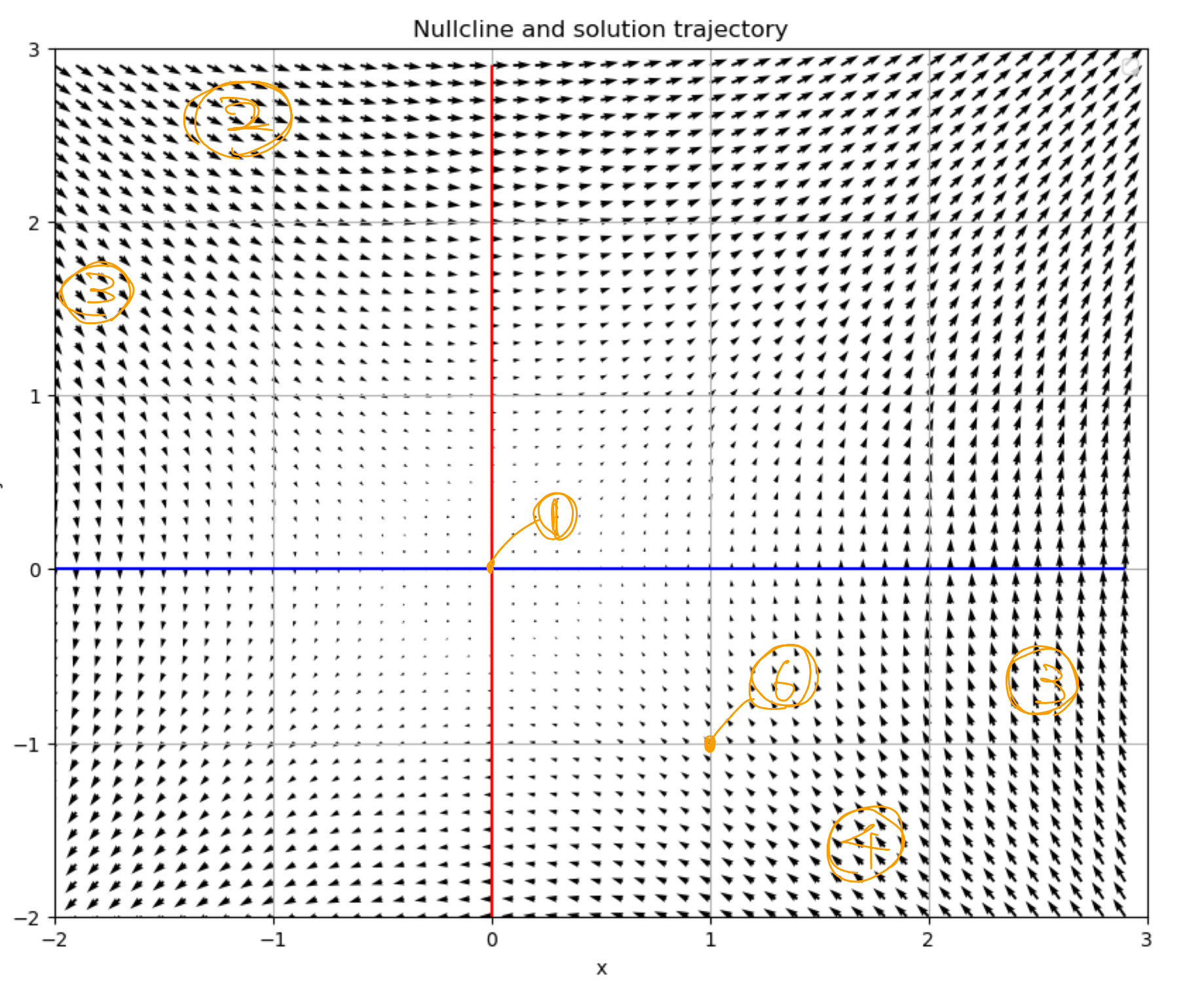
1. (0, 0)のとき

初期値から動いていないことがわかる。ヌルクラインが交わる点は鞍点といいtにより移動せずにその場に留まる ただ、今回はベクトル場からわかるように不安定な固定点である

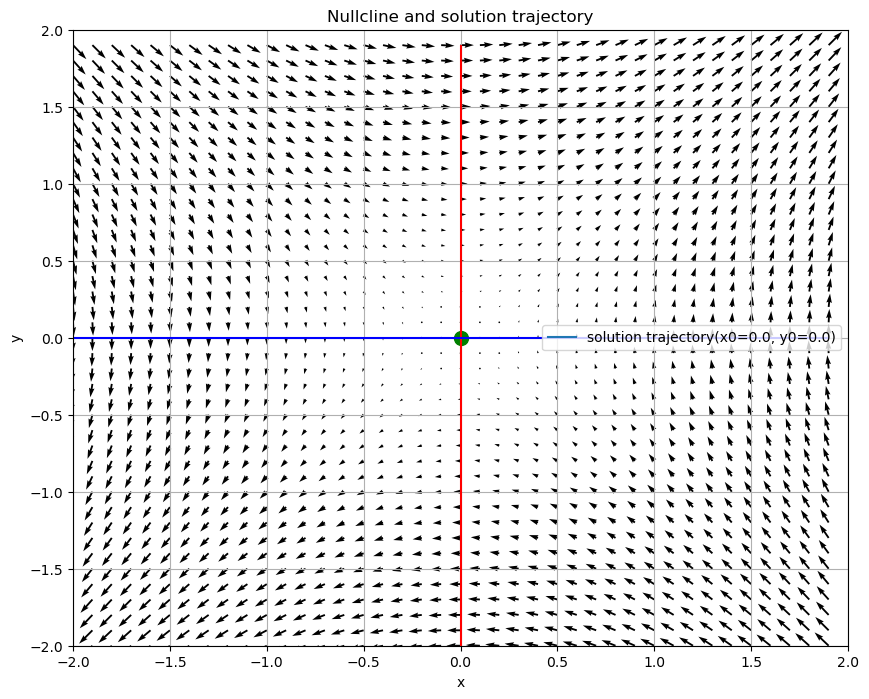
2. 2の領域の場合 今回は(-1, 2)とすると

めんどくさくなったので、ここで細かい説明は区切るが、他の領域の図はこのようになる

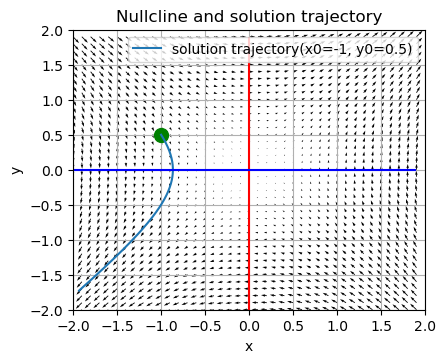
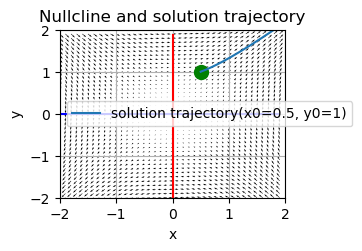
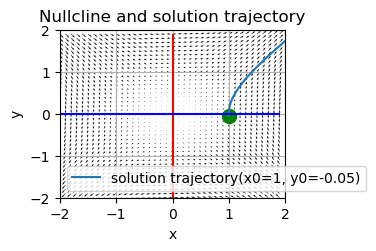
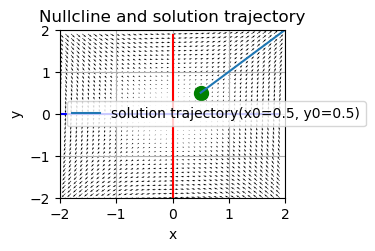bc<0のとき 微分方程式の係数部分をbc<0とすると楕円状の解軌道になる a = d = 0, b = 1.5, c = -1

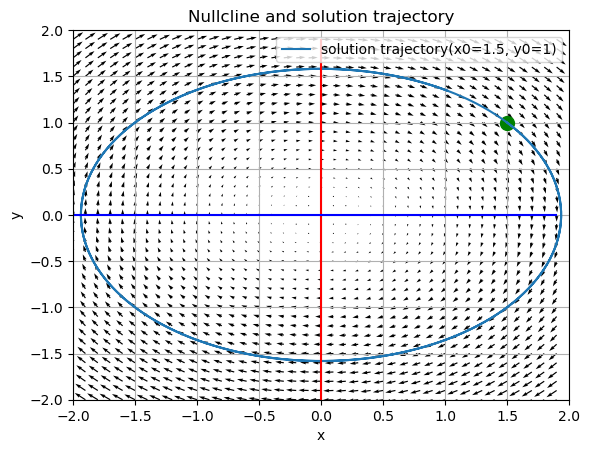a=d=0, b, c<0の時

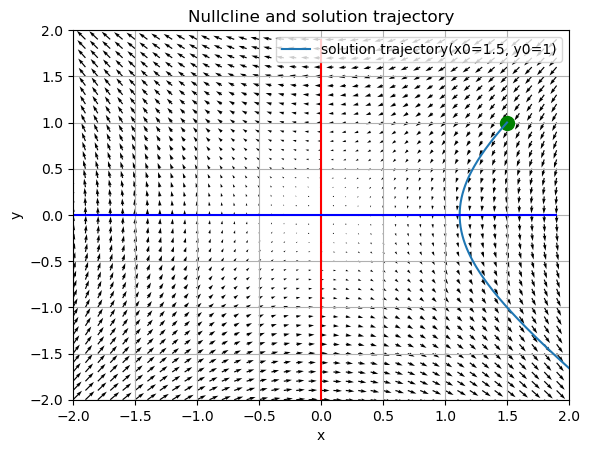
b, c > 0の時と同様、双曲線型

ちなみに a = -2, b = 2, -3, 1の場合螺旋状に原点へ収束していく